Sparse Computation in DNNs
It has been demonstrated that the weight matrices can be relatively sparse (i.e., only 10% nonzero) without significantly impacting the model performance [1]. However, the techniques for learning such sparse weight matrices often lead to arbitrary positioning of the nonzero weight values in each matrix. This makes efficient computation difficult to implement due to higher routing complexity associated with these arbitrary positions. Alternatively, more recent work has been done on block-sparse algorithms[2], which can be implemented efficiently in GPUs.
My work in this area has focused on enforcing a special type of structured sparsity that can be deployed efficiently in systolic arrays. This structure is more fine-grained than the block-sparse approach. Some excellent follow-up work has been done based on this type of fine-grained sparsity[3, 4], and appears to be enabled somewhat in latest NVIDIA GPU Tensor Cores.
Relevant Publications
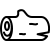
Accelerating DNN Training with Structured Data Gradient Pruning
B. McDanel, H. Dinh, J. Magallanes
International Conference on Pattern Recognition (ICPR), 2022.
preprint
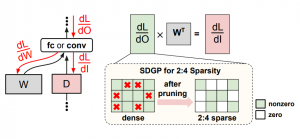
Saturation RRAM Leveraging Bit-level Sparsity Resulting from Term Quantization
B. McDanel, H. T. Kung, S. Zhang
IEEE International Symposium on Circuits and Systems (ISCAS), 2021
paper
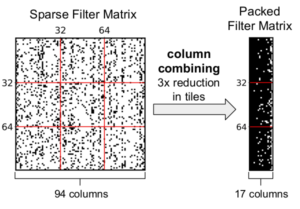
Packing Sparse Convolutional Neural Networks for Efficient Systolic Array Implementations: Column Combining Under Joint Optimization
H. T. Kung, B. McDanel, and S. Zhang
24th ACM International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS), 2019
paper | code
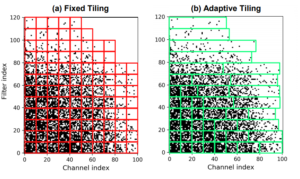
Adaptive Tiling: Applying Fixed-size Systolic Arrays To Sparse Convolutional Neural Networks
H. T. Kung, B. McDanel, S. Zhang
International Conference on Pattern Recognition (ICPR), 2018
paper